Pythagoras’ Theorem
Using Pythagoras’ Theorem to find diagonal lengths
Follow-up activities
-
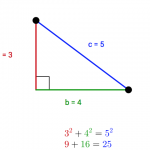 Interactive: Pythagoras’ Theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. Drag the corners to change the side lengths.
Interactive: Pythagoras’ Theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. Drag the corners to change the side lengths.
Proving Pythagoras’ Theorem
Instructions
How does Pythagoras’ Theorem work?
- Redraw the diagram and label clearly.
- Annotate the diagram with all you know about the lengths, angles, shapes and areas on the diagram.
- Can you prove that c2 = a2 + b2?
Required Materials
Extra Resources
Trigonometry
Triangle measurement
Instructions
Trigonometry literally means “triangle measurement”.
- Measure the sides of your group of eight similar triangles (different sizes but same shape). What makes them similar?
- Record your measurements in the table. Record the angle size of your triangles.
- Calculate the ratios of each pair of sides (three sides means three pairs). Do you notice a pattern?
- Calculate the mean (average) of the ratios. Share your results with the class and construct a graph of the ratios.
- Use a calculator to find the sine, cosine and tangent (sin, cos, tan) of your angle size. What do you notice?
- If the ratios for a certain angle size are always the same, we can use these relationships to find an unknown side or angle. Would you prefer to repeat this kind of triangle measurement or use a calculator?
Required Materials
Follow-up activities
-
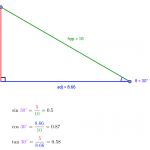 Interactive: Trigonometric Ratios The three trigonometric ratios represented on a right-angled triangle. Drag the corners to see how changing the scale and angle size changes the ratios.
Interactive: Trigonometric Ratios The three trigonometric ratios represented on a right-angled triangle. Drag the corners to see how changing the scale and angle size changes the ratios. - Skills practice: Using the Trig Ratios
Extra Resources
Use Trigonometry to calculate the size of things
Choose large objects around the school, measure sides and angles to calculate ‘unmeasurable’ sides and angles (at least one of each).
